Domov \ Dokumentácia \ Pre učiteľa informatiky

Pri použití materiálov z tejto stránky - a umiestnenie banneru je POVINNÉ!!!

Binárna aritmetika

Čísla, ktoré sme zvyknutí používať, sa nazývajú desiatkové a aritmetika, ktorú používame, sa nazýva aj desiatkové. Každé číslo sa totiž môže skladať zo sady čísiel obsahujúcich 10 znakov – číslic – „0123456789“.

Matematika sa vyvinula tak, že táto konkrétna množina sa stala hlavnou, ale desiatková aritmetika nie je jediná. Ak vezmeme iba päť číslic, potom na ich základe môžeme zostaviť päťcifernú aritmetiku a zo siedmich číslic sedemcifernú aritmetiku. V oblastiach vedomostí súvisiacich s výpočtovou technikou sa často používa aritmetika, v ktorej čísla pozostávajú zo šestnástich číslic; podľa toho sa táto aritmetika nazýva hexadecimálna. Aby sme pochopili, čo je číslo v desiatkovej aritmetike, najprv zistíme, čo je číslo v desiatkovej aritmetike.

Vezmite si napríklad číslo 246. Tento zápis znamená, že v čísle sú dve stovky, štyri desiatky a šesť jednotiek. Preto môžeme napísať nasledujúcu rovnosť:

246 = 200 + 40 + 6 = 2 * 10 2 + 4 * 10 1 + 6 * 10 0

Znamienko rovnosti oddeľuje tri spôsoby zápisu toho istého čísla. Teraz je pre nás najzaujímavejšia tretia forma zápisu: 2 * 10 2 + 4 * 10 1 + 6 * 10 0 . Je štruktúrovaný nasledovne:

Naše číslo má tri číslice. Vedúca číslica "2" je číslo 3. Takže sa vynásobí 10 na druhú mocninu. Ďalšia číslica „4“ má poradové číslo 2 a v prvej sa vynásobí 10. Už je jasné, že číslice sa násobia desiatimi na mocninu o jednu menej, ako je poradové číslo číslice. Po pochopení vyššie uvedeného si môžeme zapísať všeobecný vzorec na vyjadrenie desatinného čísla. Dajme číslo s N číslicami. I-tu číslicu budeme označovať i. Potom možno číslo zapísať v nasledujúcom tvare: a n a n-1 ....a 2 a 1 . Toto je prvý formulár a tretí vstupný formulár bude vyzerať takto:

a n a n-1 ....a 2 a 1 = a n * 10 n-1 + a n-1 * 10 n-2 + .... + a 2 * 10 1 + a 1 * 10 0

kde a i je znak z množiny "0123456789"

Úloha desiatky je na tejto nahrávke veľmi jasne viditeľná. Desať je základom pre tvorbu čísel. A mimochodom, nazýva sa to „základ číselného systému“ a samotný číselný systém je dôvod, prečo sa nazýva „desiatkový“. Samozrejme, že číslo desať nemá žiadne špeciálne vlastnosti. Desiatku môžeme jednoducho nahradiť ľubovoľným iným číslom. Napríklad číslo v päťmiestnej číselnej sústave možno zapísať takto:

a n a n-1 ....a 2 a 1 = a n * 5 n-1 + a n-1 * 5 n-2 + .... + a 2 * 5 1 + a 1 * 5 0

kde a i je znak z množiny "01234"

Vo všeobecnosti nahradíme 10 akýmkoľvek iným číslom a získame úplne inú číselnú sústavu a inú aritmetiku. Najjednoduchšiu aritmetiku získame, ak sa 10 nahradí 2. Výsledná číselná sústava sa nazýva binárna a číslo v nej je definované takto:

a n a n-1 ....a 2 a 1 = a n * 2 n-1 + a n-1 * 2 n-2 + .... + a 2 * 2 1 + a 1 * 2 0

kde a i je znak z množiny "01"

Tento systém je najjednoduchší zo všetkých možných, keďže v ňom je každé číslo tvorené len z dvoch číslic 0 a 1. Je jasné, že jednoduchší už ani nemôže byť. Príklady binárnych čísel: 10, 111, 101.

Veľmi dôležitá otázka. Môže byť binárne číslo reprezentované ako desiatkové číslo a naopak, môže byť desiatkové číslo reprezentované ako binárne číslo.

Binárne na desiatkové. Je to veľmi jednoduché. Spôsob takéhoto prekladu je daný naším spôsobom zápisu čísel. Vezmime si napríklad nasledujúce dvojkové číslo 1011. Rozviňme ho na mocniny dvojky. Získame nasledovné:

1011 = 1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0

Vykonajte všetky zaznamenané akcie a získajte:

1 * 2 3 + 0 * 2 2 + 1 * 2 1 + 1 * 2 0 = 8 + 0+ 2 + 1 = 11. Dostaneme teda, že 1011 (binárne) = 11 (desiatkové). Mierna nepríjemnosť binárneho systému je okamžite viditeľná. Rovnaké číslo, ktoré je zapísané v desiatkovej sústave jednou číslicou v dvojkovej sústave, potrebuje na svoj zápis štyri číslice. Ale toto je cena za jednoduchosť (nič nie je zadarmo). Binárny systém však poskytuje obrovský zisk v aritmetických operáciách. A to uvidíme neskôr.

Vyjadrite nasledujúce binárne čísla ako desatinné.

a) 10010 b) 11101 c) 1010 c) 1110 d) 100011 e) 1100111 f) 1001110

Sčítanie binárnych čísel.

Metóda sčítania stĺpcov je vo všeobecnosti rovnaká ako pre desatinné číslo. To znamená, že sčítanie sa vykonáva po bitoch, počnúc najmenej významnou číslicou. Ak je pri sčítaní dvoch číslic SÚČET väčší ako deväť, zapíše sa číslica = SÚČET - 10 a CELÁ ČASŤ (SÚČET / 10) sa pripočíta ako najvýznamnejšia číslica. (Pridajte niekoľko čísel do stĺpca, nezabudnite, ako sa to robí.) To isté s binárnym číslom. Pridajte jeden po druhom, počnúc najnižšou číslicou. Ak je výsledok väčší ako 1, zapíše sa 1 a k najvýznamnejšej číslici sa pridá 1 (hovorí sa „z hlavy“).

Urobme príklad: 10011 + 10001.

Prvá kategória: 1+1 = 2. Píšeme 0 a 1, ako nás napadne.

Druhá kategória: 1+0+1 (zapamätaná jednotka) =2. Zapisujeme si 0 a 1, prišlo na um.

Tretia kategória: 0+0+1 (zapamätaná jednotka) = 1. Napíšte 1.

Štvrtá kategória 0+0=0. Píšeme 0.

Piata kategória 1+1=2. Zapíšeme 0 a pripočítame 1 k šiestej číslici.

Prevedieme všetky tri čísla do desiatkovej sústavy a skontrolujeme správnosť sčítania.

10011 = 1*2 4 + 0*2 3 + 0*2 2 + 1*2 1 + 1*2 0 = 16 + 2 + 1 =19

10001 = 1*2 4 + 0*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 16 + 1 = 17

100100 = 1*2 5 + 0*2 4 + 0*2 3 + 1*2 2 + 0*2 1 + 0*2 0 =32+4=36

17 + 19 = 36 správna rovnosť

Príklady nezávislých riešení:

a) 11 001 + 101 =

b) 11001 +11001 =

c) 1001 + 111 =

e) 10 011 + 101 =

e) 11011 + 1111 =

e) 11111 + 10011 =

Ako previesť desiatkové číslo na binárne. Ďalšou operáciou je odčítanie. Ale touto operáciou sa budeme zaoberať o niečo neskôr a teraz zvážime metódu prevodu desatinného čísla na binárne.

Aby bolo možné previesť desiatkové číslo na binárne, musí byť rozšírené na mocniny dvoch. Ale ak sa rozšírenie v mocninách desať dosiahne okamžite, potom to, ako expandovať v mocninách dvoch, vyžaduje trochu premýšľania. Najprv sa pozrime, ako to urobiť pomocou metódy výberu. Zoberme si desatinné číslo 12.

Krok jedna. 2 2 = 4, to nestačí. Tiež 2 3 = 8 nestačí, ale 2 4 = 16 je už veľa. Preto necháme 2 3 =8. 12 - 8 = 4. Teraz to musíte vyjadriť ako mocninu dvoch 4.

Krok dva. 4 = 22.

Potom je naše číslo 12 = 2 3 + 2 2. Najvyššia číslica má číslo 4, najvyšší stupeň = 3, preto musia existovať členy s mocninami dvoch 1 a 0. Tie však nepotrebujeme, aby sme sa zbavili nepotrebných stupňov a nechali potrebné , zapíšeme číslo takto: 1*2 3 + 1* 2 2 +0*2 1 + 0*2 0 = 1100 - toto je binárne vyjadrenie čísla 12. Je ľahké si všimnúť, že každá nasledujúca mocnina je najväčšia mocnina dvojky, ktorá je menšia ako rozkladové číslo. Na konsolidáciu metódy sa pozrime na ďalší príklad. Číslo 23.

Krok 1. Najbližšia mocnina dvoch je 2 4 = 16. 23 -16 = 7.

Krok 2. Najbližšia mocnina dvoch 2 2 = 4. 7 - 4 = 3

Krok 3. Najbližšia mocnina dvoch 2 1 = 2. 3 - 2 = 1

Krok 4. Najbližšia mocnina dvoch 2 0 =1 1 - 1 =0

Dostaneme nasledujúce rozšírenie: 1*2 4 + 0*2 3 +1*2 2 +1*2 1 +1*2 0

A naše požadované binárne číslo je 10111

Vyššie diskutovaná metóda dobre rieši problém, ktorý jej bol pridelený, ale existuje metóda, ktorá je algoritmizovaná oveľa lepšie. Algoritmus pre túto metódu je napísaný nižšie:

Ak je ČÍSLO väčšie ako nula, urobte to

NEXT DIGIT = zvyšok ČÍSLA delený 2

NUMBER = celá časť čísla NUMBER delená 2

Keď tento algoritmus dokončí svoju prácu, postupnosť vypočítaných NEXT DIGITS bude predstavovať binárne číslo. Pracujme napríklad s číslom 19.

Začiatok algoritmu ČÍSLO = 19

ĎALŠIA ČÍSLICA = 1

ĎALŠIA ČÍSLICA = 1

ĎALŠIA ČÍSLICA = 0

ĎALŠIA ČÍSLICA = 0

ĎALŠIA ČÍSLICA = 1

V dôsledku toho máme nasledujúce číslo 10011. Všimnite si, že dve diskutované metódy sa líšia v poradí, v ktorom sa získajú ďalšie číslice. Pri prvom spôsobe je prvá prijatá číslica najvýznamnejšou číslicou binárneho čísla a pri druhom spôsobe je prvá prijatá číslica, naopak, najmenej významná.

Preveďte desatinné čísla na binárne dvoma spôsobmi

a) 14 b) 29 c) 134 d) 158 f) 1190 g) 2019

Ako previesť zlomok na desatinné číslo.

Je známe, že každé racionálne číslo môže byť reprezentované ako desatinný a obyčajný zlomok. Obyčajný zlomok, teda zlomok tvaru A/B, môže byť pravidelný a nesprávny. Zlomok sa nazýva vlastný, ak A<В и неправильной если А>IN.

Ak je racionálne číslo reprezentované nesprávnym zlomkom a čitateľ zlomku je delený menovateľom celkom, potom je toto racionálne číslo celé číslo, vo všetkých ostatných prípadoch sa objaví zlomková časť. Zlomková časť je často veľmi dlhé číslo a dokonca nekonečné (nekonečný periodický zlomok, napríklad 20/6), takže v prípade zlomkovej časti nemáme za úlohu len preložiť jednu reprezentáciu do druhej, ale preložiť pomocou určitú presnosť.

Pravidlo presnosti. Predpokladajme, že ste dostali desatinné číslo, ktoré možno znázorniť ako desatinný zlomok s presnosťou na N číslic. Aby bolo zodpovedajúce binárne číslo rovnako presné, je potrebné doň napísať znamienka M, aby

Teraz sa pokúsme získať pravidlo prekladu a najprv sa pozrime na príklad 5 401

Riešenie:

Celú časť získame podľa nám už známych pravidiel a rovná sa binárnemu číslu 101. A zlomkovú časť rozšírime o mocniny 2.

Krok 1: 2-2 = 0,25; 0,401 - 0,25 = 0,151. - toto je zvyšok.

Krok 2: Teraz musíme reprezentovať 0,151 ako mocninu dvoch. Urobme toto: 2 -3 = 0,125; 0,151 - 0,125 = 0,026

Pôvodná zlomková časť teda môže byť reprezentovaná ako 2 -2 +2 -3. To isté možno zapísať do tohto binárneho čísla: 0,011. Prvá zlomková číslica je nula, pretože v našom rozšírení neexistuje mocnina 2 -1.

Z prvého a druhého kroku je jasné, že toto znázornenie nie je presné a môže byť žiaduce pokračovať v rozširovaní. Pozrime sa na pravidlo. Hovorí, že potrebujeme toľko znakov M, že 10 3 je menej ako 2 M. To znamená 1000<2 M . То есть в двоичном разложении у нас должно быть не менее десяти знаков, так как 2 9 = 512 и только 2 10 = 1024. Продолжим процесс.

Krok 3: Teraz pracujeme s číslom 0,026. Najbližšia mocnina dvojky k tomuto číslu je 2 -6 = 0,015625; 0,026 - 0,015625 = 0,010375 Teraz je naše presnejšie binárne číslo: 0,011001. Za desatinnou čiarkou je už šesť miest, ale to je ešte málo, takže robíme ešte jeden krok.

Krok 4: Teraz pracujeme s číslom 0,010375. Najbližšia mocnina dvojky k tomuto číslu je 2 -7 = 0,0078125;

0,010375 - 0,0078125 = 0,0025625

Krok 5: Teraz pracujeme s číslom 0,0025625. Najbližšia mocnina dvojky k tomuto číslu je 2 -9 = 0,001953125;

0,0025625 - 0,001953125 = 0,000609375

Posledný výsledný zvyšok je menší ako 2 -10 a ak by sme chceli pokračovať v aproximácii pôvodného čísla, potrebovali by sme 2 -11, čo však už presahuje požadovanú presnosť, a preto je možné výpočty zastaviť a výslednú binárnu reprezentáciu zlomkovú časť možno zapísať.

0,401 = 0,011001101

Ako vidíte, prevod zlomkovej časti desatinného čísla na binárne je o niečo zložitejší ako prevod celej časti. Tabuľka mocnin dvojky na konci prednášky.

Teraz si zapíšme algoritmus konverzie:

Počiatočné údaje algoritmu: Prostredníctvom A budeme označovať pôvodný správny desatinný zlomok zapísaný v desatinnom tvare. Nech tento zlomok obsahuje N znakov.

Algoritmus

Činnosť 1. Určte počet požadovaných dvojkových číslic M z nerovnosti 10 N< 2 M

Činnosť 2: Cyklus na výpočet číslic binárnej reprezentácie (číslice po nule). Číselné číslo bude označené symbolom K.

1. Číselné číslo = 1
2. Ak 2-K > A

Potom k binárnemu číslu pridáme nulu

• pridajte 1 k binárnemu číslu
• A = A-2-K

1. K = K + 1
2. Ak K > M

• potom je algoritmus dokončený
• V opačnom prípade prejdite na bod 2.

Previesť desatinné čísla na binárne

a) 3,6 b) 12,0112 c) 0,231 d) 0,121 d) 23,0091

Odčítanie binárnych čísel. Odčítať budeme aj čísla v stĺpci a všeobecné pravidlo je rovnaké ako pri desatinných číslach, odčítanie sa vykonáva po bitoch a ak je na mieste málo, tak v najvyššom. Poďme vyriešiť nasledujúci príklad:

Prvá kategória. 1 - 0 = 1. Zapisujeme si 1.

Druhá kategória 0-1. Jeden chýba. Obsadzujeme ju v seniorskej kategórii. Jednotka z vyššej číslice prechádza do nižšej, ako sú dve jednotky (pretože horná číslica je reprezentovaná dvojkou vyššieho stupňa) 2-1 = 1. Zapisujeme si 1.

Tretia kategória. Obsadili sme jednotku tejto hodnosti, takže teraz v hodnosti 0 je potrebné obsadiť jednotku najvyššej hodnosti. 2-1 = 1. Zapisujeme si 1.

Výsledok skontrolujeme v desiatkovej sústave

1101 - 110 = 13 - 6 = 7 (111) Správna rovnosť.

Ďalší zaujímavý spôsob vykonávania odčítania zahŕňa koncept kódu dvojkového doplnku, ktorý vám umožňuje zredukovať odčítanie na sčítanie. Výsledok čísla v dvojkovom doplnkovom kóde je veľmi jednoduchý: vezmeme číslo, nuly nahradíme jednotkami, naopak, nahradíme jednotky nulami a k ​​najmenej významnej číslici pripočítame jednotku. Napríklad 10010, doplnkový kód bude 011011.

Pravidlo odčítania prostredníctvom dvojkového doplnku hovorí, že odčítanie môže byť nahradené sčítaním, ak je odpočet nahradený číslom v dvojkovom doplnku.

Príklad: 34 – 22 = 12

Napíšme tento príklad v binárnom tvare. 100010 – 10110 = 1100

Doplnkový kód čísla 10110 bude takýto

01001 + 00001 = 01010. Potom je možné pôvodný príklad nahradiť sčítaním takto: 100010 + 01010 = 101100 Ďalej je potrebné vyradiť jednu jednotku s najvýznamnejšou číslicou. Ak to urobíme, dostaneme 001100. Vyhoďme bezvýznamné nuly a dostaneme 1100, to znamená, že príklad bol vyriešený správne

Vykonajte odčítanie. Zvyčajným spôsobom a v dodatočnom kóde po predchádzajúcej konverzii desiatkových čísel na binárne:

Skontrolujte prevedením binárneho výsledku do desiatkovej číselnej sústavy.

Násobenie v dvojkovej číselnej sústave.

Najprv zvážte nasledujúci zaujímavý fakt. Na vynásobenie binárneho čísla 2 (desatinná dvojka je v dvojkovej sústave 10) stačí pridať jednu nulu naľavo od násobeného čísla.

Príklad. 10101 * 10 = 101010

Vyšetrenie.

10101 = 1*2 4 + 0*2 3 + 1*2 2 + 0*2 1 +1*2 0 = 16 + 4 + 1 = 21

101010 =1*2 5 + 0*2 4 + 1*2 3 + 0*2 2 +1*2 1 +0*2 0 = 32 + 8 + 2 = 42

Ak si spomenieme, že každé binárne číslo možno rozšíriť na mocniny dvoch, potom je jasné, že násobenie v systéme binárnych čísel sa redukuje na násobenie 10 (to znamená desatinnou čiarkou 2), a preto je násobenie sériou po sebe idúcich smeny. Všeobecným pravidlom je, že rovnako ako v prípade desiatkových čísel sa binárne násobenie vykonáva po bitoch. A za každú číslicu druhého násobiteľa sa napravo od prvého násobiteľa pridá jedna nula. Príklad (zatiaľ nie je v stĺpci):

1011 * 101 Toto násobenie možno zredukovať na súčet trojciferných násobení:

1011 * 1 + 1011 * 0 + 1011 * 100 = 1011 +101100 = 110111 To isté možno zapísať do stĺpca, ako je tento:

Vyšetrenie:

101 = 5 (desatinné)

1011 = 11 (desatinné)

110111 = 55 (desatinné)

5*11 = 55 správna rovnosť

Rozhodnite sa sami

a) 1101 * 1110 =

b) 1010 x 110 =

e) 101011 * 1101 =

e) 10 010 * 1 001 =

Poznámka: Mimochodom, tabuľka násobenia v binárnom systéme pozostáva iba z jednej položky 1 * 1 = 1

Delenie v dvojkovej číselnej sústave.

Pozreli sme sa už na tri akcie a myslím si, že už je jasné, že vo všeobecnosti sa akcie s binárnymi číslami líšia od akcií s desatinnými číslami. Jediný rozdiel je v tom, že sú tam dve čísla a nie desať, ale to len zjednodušuje aritmetické operácie. S delením je situácia rovnaká, ale pre lepšie pochopenie si algoritmus delenia rozoberieme podrobnejšie. Predpokladajme, že potrebujeme rozdeliť dve desatinné čísla, napríklad 234 delené 7. Ako to urobíme.

Vyberieme smerom doprava (od najvýznamnejšej číslice) taký počet číslic, aby výsledné číslo bolo čo najmenšie a zároveň väčšie ako deliteľ. 2 je menšie ako deliteľ, preto potrebujeme číslo 23. Výsledné číslo potom delíme deliteľom so zvyškom. Dostaneme nasledujúci výsledok:

Popísanú operáciu opakujeme, kým výsledný zvyšok nebude menší ako deliteľ. Keď sa to stane, číslo získané pod čiarou je kvocient a posledný zvyšok je zvyšok operácie. Takže operácia delenia binárneho čísla sa vykonáva presne rovnakým spôsobom. Vyskúšajme

Príklad: 10010111 / 101

Hľadáme číslo, ktorého prvá číslica je väčšia ako deliteľ. Ide o štvormiestne číslo 1001. Je vytlačené tučným písmom. Teraz musíte nájsť deliteľa pre vybrané číslo. A tu opäť vyhrávame v porovnaní s desiatkovou sústavou. Faktom je, že vybraný deliteľ je nevyhnutne číslo a my máme iba dve čísla. Keďže 1001 je jednoznačne väčšie ako 101, potom je s deliteľom všetko jasné: 1. Vykonajte krok operácie.

Takže zvyšok dokončenej operácie je 100. To je menej ako 101, takže na vykonanie kroku druhého delenia musíte pridať ďalšiu číslicu k 100, toto je číslica 0. Teraz máme nasledujúce číslo:

1000 je väčšie ako 101, preto v druhom kroku opäť pripočítame k podielu číslo 1 a dostaneme nasledujúci výsledok (pre úsporu miesta hneď vynecháme ďalšiu číslicu).

Tretí krok. Výsledné číslo 110 je väčšie ako 101, preto v tomto kroku napíšeme do kvocientu 1. Dopadne to takto:

Výsledné číslo 11 je menšie ako 101, preto do podielu napíšeme číslo 0 a ďalšie číslo znížime nadol. Dopadá to takto:

Výsledné číslo je väčšie ako 101, preto do kvocientu zapíšeme číslo 1 a akcie vykonáme znova. Ukazuje sa tento obrázok:

1

0

Výsledný zvyšok 10 je menší ako 101, ale v dividende sa nám minuli číslice, takže 10 je konečný zvyšok a 1110 je požadovaný kvocient.

Pozrime sa na desatinné čísla

Toto uzatvára popis najjednoduchších aritmetických operácií, ktoré potrebujete vedieť, aby ste mohli používať binárnu aritmetiku, a teraz sa pokúsime odpovedať na otázku „Prečo je potrebná binárna aritmetika? Samozrejme, už vyššie sa ukázalo, že zápis čísla do dvojkovej sústavy výrazne zjednodušuje aritmetické operácie, no zároveň sa samotný záznam značne predĺži, čo znižuje hodnotu výsledného zjednodušenia, preto je potrebné hľadať napr. úlohy, ktorých riešenie je oveľa jednoduchšie v binárnych číslach.

Úloha 1: Získanie všetkých vzoriek

Veľmi často sa vyskytujú problémy, pri ktorých musíte byť schopní zostaviť všetky možné kombinácie z danej množiny objektov. Napríklad táto úloha:

Vzhľadom na veľkú hromadu kameňov usporiadajte kamene do dvoch kôp tak, aby ich hmotnosť bola čo najviac rovnaká.

Táto úloha môže byť formulovaná nasledovne:

Nájdite výber kameňov z veľkej kopy tak, aby sa ich celková hmotnosť čo najmenej líšila od polovice hmotnosti veľkej kopy.

Úloh tohto druhu je pomerne veľa. A všetky sa scvrkávajú, ako už bolo povedané, na schopnosť získať všetky možné kombinácie (ďalej ich budeme nazývať vzorky) z danej množiny prvkov. A teraz sa pozrieme na všeobecnú metódu získania všetkých možných vzoriek pomocou operácie binárneho sčítania. Začnime príkladom. Nech existuje súbor troch predmetov. Skonštruujme všetky možné vzorky. Predmety budeme označovať sériovými číslami. To znamená, že existujú nasledujúce položky: 1, 2, 3.

Vzorky: (0, 0, 1); (0, 1, 0); (0, 1, 1); (100); (1, 0, 1); (1, 1, 0); (1, 1, 1);

Ak je pozícia s nasledujúcim číslom jedna, znamená to, že prvok s číslom rovným tejto pozícii je prítomný vo výbere a ak je nula, prvok nie je prítomný. Napríklad vzorka (0, 1, 0); pozostáva z jedného prvku s číslom 2 a výber je (1, 1, 0); pozostáva z dvoch prvkov s číslami 1 a 2.

Tento príklad jasne ukazuje, že vzorka môže byť reprezentovaná ako binárne číslo. Okrem toho je ľahké vidieť, že všetky možné jedno, dvoj a trojmiestne binárne čísla sú napísané vyššie. Prepíšme ich takto:

001; 010; 011; 100; 101; 110; 111

1; 10; 11; 100; 101; 110; 111

Dostali sme sériu po sebe idúcich binárnych čísel, z ktorých každé sa získa z predchádzajúceho pridaním jedného. Môžete to skontrolovať. Pomocou tohto pozorovaného vzoru môžeme zostaviť nasledujúci algoritmus na získanie vzoriek.

Vstupné údaje algoritmu

Daný súbor objektov N - kusov. Ďalej budeme túto množinu nazývať množina počiatočných prvkov. Očíslujme všetky prvky pôvodnej množiny od 1 do N. Z N bezvýznamných núl urobme dvojkové číslo. 0000… 0 N Toto nulové binárne číslo bude označovať nulovú vzorku, s ktorou začne proces vzorkovania. Číslice čísla sa počítajú sprava doľava, to znamená, že číslica úplne vľavo je najvýznamnejšia.

Dohodnime sa, že toto binárne číslo budeme označovať veľkými písmenami BINARY

Algoritmus

Ak BINÁRNE číslo pozostáva výlučne z jednotiek

Potom algoritmus zastavíme

• Jedničku pripočítame k BINÁRNEMU číslu podľa pravidiel binárnej aritmetiky.
• Z výsledného BINARY čísla urobíme ďalšiu vzorku, ako je popísané vyššie.

Úloha 2: Nájdenie veľkých prvočísel

Na začiatok si pripomeňme, že prvočíslo je prirodzené číslo, ktoré je deliteľné iba 1 a sebou samým. Príklady prvočísel: 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31

Hľadanie veľkých prvočísel je veľmi dôležitý matematický problém. Veľké prvočísla sú potrebné pre niektoré šifrovacie algoritmy na bezpečné šifrovanie správ. Navyše sú potrebné nielen veľké počty, ale aj veľmi veľké. Čím väčšie číslo, tým spoľahlivejšia je šifra postavená na tomto čísle.

Poznámka. Silná šifra je šifra, ktorej rozlúštenie trvá veľmi dlho.

prečo? Prvočíslo funguje ako kľúč na šifrovanie a dešifrovanie. Navyše vieme, že prvočísla sa v rade prirodzených čísel veľmi často nevyskytujú. Medzi prvou tisíckou ich je pomerne veľa, potom ich počet začína rýchlo klesať. Ak teda za kľúč zoberieme nie príliš veľké číslo, dešifrovač sa k nemu aj pomocou nie veľmi rýchleho počítača dostane (vyskúšaním všetkých jednoduchých čísel za sebou ako kľúča) v obmedzenom čas.

Pomerne spoľahlivý kód možno získať, ak si vezmete jednoduchý, napríklad 150 znakov. Nájsť taký jednoduchý však nie je také jednoduché. Predpokladajme, že určité číslo A (veľmi veľké) je potrebné skontrolovať na primálnosť. Je to rovnaké ako pri hľadaní jeho deliteľov. Ak môžeme nájsť deliteľa v rozsahu od 2 do druhej odmocniny z A, potom to nie je prvočíslo. Odhadnime počet čísel, ktoré je potrebné otestovať na schopnosť rozdeliť číslo A.

Povedzme, že číslo A má 150 číslic. Jeho druhá odmocnina bude obsahovať najmenej 75 znakov. Na pretriedenie takého množstva možných deliteľov potrebujeme veľmi výkonný počítač a veľa času, čo znamená, že problém je prakticky neriešiteľný.

Ako sa s tým vysporiadať.

Po prvé, môžete sa naučiť rýchlo kontrolovať deliteľnosť jedného čísla druhým a po druhé môžete skúsiť vybrať číslo A tak, aby bolo prvočíslo s vysokou pravdepodobnosťou. Ukazuje sa, že je to možné. Matematik Mersen objavil čísla nasledujúceho tvaru

Sú jednoduché s vysokou mierou pravdepodobnosti.

Aby sme pochopili frázu napísanú vyššie, spočítajme, koľko prvočísel je v prvej tisícke a koľko Mersenových čísel je prvočísel v tej istej tisícke. Mersenove čísla v prvej tisícke sú teda nasledovné:

2 1 - 1 = 1 ; 2 2 -1 = 3 ; 2 3 - 1 = 7 ; 2 4 - 1 = 15; 2 5 - 1 = 31 ; 2 6 -1 = 63;

2 7 - 1 =127 ; 2 8 -1 = 255; 2 9 - 1 = 511;

Prvočísla sú vyznačené tučným písmom. Na 9 Mersenových čísel pripadá 5 prvočísel. V percentách je to 5/9*100 = 55,6 %. Zároveň na každých 1000 prvých prirodzených čísel pripadá len 169 prvočísel. V percentách je to 169/1000*100 = 16,9 %. To znamená, že v prvej tisícke v percentuálnom vyjadrení sa prvočísla medzi Mersenovými číslami nachádzajú takmer 4-krát častejšie ako medzi jednoduchými prirodzenými číslami.

___________________________________________________________

Teraz si zoberme konkrétne Mersenovo číslo, napríklad 2 4 - 1. Zapíšme ho ako binárne číslo.

2 4 - 1 = 10000 - 1 = 1111

Zoberme si nasledujúce Mersenovo číslo 2 5 -1 a napíšme ho ako binárne číslo. Získame nasledovné:

2 5 -1 = 100000 - 1 = 11111

Už teraz je jasné, že všetky Mersenove čísla sú postupnosťou jednotiek a táto skutočnosť sama o sebe dáva veľký zisk. Po prvé, v dvojkovej číselnej sústave je veľmi jednoduché získať ďalšie Mersenovo číslo, stačí k ďalšiemu číslu pripočítať jedničku a po druhé, hľadanie deliteľov v dvojkovej sústave je oveľa jednoduchšie ako v desiatkovej sústave.

Rýchla konverzia z desatinných miest na binárne

Jedným z hlavných problémov pri používaní binárneho číselného systému je obtiažnosť prevodu desiatkového čísla na binárne. Toto je dosť náročná úloha. Samozrejme, nie je príliš ťažké preložiť malé čísla s tromi alebo štyrmi číslicami, ale pre desatinné čísla s 5 alebo viacerými číslicami je to už ťažké. To znamená, že potrebujeme spôsob, ako rýchlo previesť veľké desatinné čísla na binárne.

Túto metódu vynašiel francúzsky matematik Legendre. Dajme napríklad číslo 11183445. Vydelíme ho 64, dostaneme zvyšok 21 a podiel je 174741. Toto číslo opäť vydelíme 64, dostaneme zvyšok 21 a podiel 2730. , 2730 delené 64 dáva zvyšok 42 a kvocient 42, ale 64 v binárnom systéme je 1 000 000, 21 v binárnom je 10101 a 42 je 101010, preto je pôvodné číslo zapísané v binárnom formáte takto:

101010 101010 010101 010101

Aby to bolo jasnejšie, uvádzame ďalší príklad s menším číslom. Preveďme binárne znázornenie čísla 235. Rozdeľme 235 číslom 64 so zvyškom. Dostaneme:

QUANTIATE = 3, binárne 11 alebo 000011

ZOSTATOK = 43, binárne 101011

Potom 235 = 11101011. Pozrime sa na tento výsledok:

11101011 = 2 7 + 2 6 + 2 5 + 2 3 + 2 1 + 2 0 = 128+64+32+8+2+1 = 235

Poznámky:

1. Je ľahké vidieť, že konečné binárne číslo zahŕňa všetky zvyšky a v poslednom kroku aj zvyšok aj kvocient.
2. Kvocient sa píše pred zvyškom.
3. Ak má výsledný kvocient alebo zvyšok v binárnom vyjadrení menej ako 6 číslic (6 núl obsahuje binárne znázornenie čísla 64 = 1000000), pripočítajú sa k nemu nevýznamné nuly.

A ešte jeden komplexnejší príklad. Číslo je 25678425.

Krok 1: 25678425 delené 64

Súkromné ​​= 401225

Zostávajúce = 25 = 011001

Krok 2: 401225 delené 64

Podiel = 6269

Zvyšok = 9 = 001001

Krok 3: 6269 delené 64

Podiel = 97

Zostávajúce = 61 = 111101

Krok 4: 97 delené 64

Podiel = 1 = 000001

Zostávajúce = 33 = 100 001

Výsledok čísla = 1,100001,111101,001001,011001

V tomto čísle sú medzivýsledky zahrnuté v ňom oddelené bodkou.

Previesť čísla na binárne znázornenie:

PRÍLOHA: TABUĽKA 1

		0,015625
		0,0078125
		0,00390625
		0,001953125
		0,0009765625
		0,00048828125
		0,000244140625
		0,0001220703125
		0,00006103515625
		0,000030517578125
		0,0000152587890625
		0,00000762939453125
		0,000003814697265625
		0,0000019073486328125
		0,00000095367431640625
		0,000000476837158203125

• oboznámi študentov s binárnou číselnou sústavou, poukáže na jej nevýhody a výhody využitia vo výpočtovej technike;
• rozvíjať logické myslenie; rozvíjať zručnosti pri vykonávaní aritmetických operácií s binárnymi číslami;
• vzbudiť záujem o danú tému.

Vyučovací softvér: PC, program Kalkulačka.

Počas vyučovania

jaOrganizovanie času

Pozdrav, kontrola neprítomných.

1. Stanovenie cieľov lekcie

- Koľko bude:

1000110 2 + 1010101 2 ; 100011110111 2 /101101 2;

1110001110 2 – 11010 2 ; 101101 2 * 100011 2

Po navrhovaných odpovediach študentov komentujem a vysvetľujem, že dnes sa v lekcii naučíme, ako správne vykonávať aritmetické operácie v binárnom číselnom systéme.

2. Človek sa v dvojkovej sústave nepočíta, pretože... nie je pre neho vhodná. Kto alebo čo ho používa na počítanie a prečo?

II.Prezentácia nového materiálu

Binárny číselný systém

Zo všetkých pozičných číselných sústav je binárna číselná sústava obzvlášť jednoduchá a preto zaujímavá.

– Aký je základ dvojkovej číselnej sústavy? (q = 2)

– Aká je rozšírená forma zápisu binárneho čísla? (A2 = a n-1 * 2 n-1 + ...a 0*2 0 + a -1 *2 -1 +...a -m *2 -m, kde a i je 1 alebo 0.)

Binárny číselný systém je už dlho predmetom veľkej pozornosti mnohých vedcov. P.S. Laplace napísal o svojom postoji k binárnemu číselnému systému veľkého matematika G.F. Leibniza: „V jeho binárnej aritmetike videl Leibniz prototyp stvorenia. Zdalo sa mu, že jednotka predstavuje božský princíp a nula predstavuje neexistenciu a že Najvyššia Bytosť vytvára všetko z neexistencie presne tak, ako jednotka a nula v jeho systéme vyjadrujú všetky čísla.“ Tieto slová zdôrazňujú úžasnú všestrannosť abecedy pozostávajúcej iba z dvoch znakov.

Binárna aritmetika.

Pre lepšie zvládnutie dvojkovej číselnej sústavy je potrebné zvládnuť vykonávanie aritmetických operácií na dvojkových číslach.

Všetky pozičné systémy sú „rovnaké“, konkrétne vo všetkých sa aritmetické operácie vykonávajú podľa rovnakých pravidiel:

• platia rovnaké aritmetické zákony: komunikatívne, asociatívne, distributívne;
• platia pravidlá sčítania, odčítania, násobenia a delenia;
• pravidlá na vykonávanie aritmetických operácií sú založené na sčítacích a násobiacich tabuľkách.

Doplnenie.

Tabuľka sčítania binárnych čísel je jednoduchá.

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
1 + 1 + 1 = 11

Keď sa pridajú dve jednotky, číslica pretečie a prenesie sa na najvýznamnejšiu číslicu. Pretečenie číslic nastane, keď sa hodnota čísla v ňom rovná alebo je väčšia ako základ.

Odčítanie.

0 – 0 = 0
0 – 1 = 11
1 – 0 = 1
1 – 1 = 0

Odčítanie viacbitových binárnych čísel prebieha v súlade s vyššie uvedenou tabuľkou odčítania, berúc do úvahy možné pôžičky od najvyšších číslic.

Násobenie.

Operácia násobenia sa vykonáva pomocou tabuľky násobenia podľa bežnej schémy (používanej v sústave desiatkových čísel) s postupným násobením násobiteľa ďalšou číslicou násobiteľa.

Pri delení podľa stĺpca musíte vykonať násobenie a odčítanie ako medzivýsledky.

III. Upevnenie toho, čo sa naučilo

Riešiť problémy.

Vykonajte sčítanie:

1001001 + 10101 (odpoveď 1011110);
101101 + 1101101 (odpoveď 10011010)
11000,11 + 11010,11 (odpoveď 110011,1)

Vykonajte odčítanie:

10001000 – 1110011 (odpoveď 10101)
1101100 – 10110110 (odpoveď – 1001010)
110101,101 – 1001,111 (101011,11)

Vykonajte násobenie:

100001*111,11 (odpoveď: 11111111,11)
10011*1111,01 (odpoveď: 100100001,11)

Vykonajte rozdelenie:

1000000 / 1110 (odpoveď:100)
11101001000/111100 (odpoveď: 11111)

IV. Zhrnutie lekcie

Hodnotenie práce žiakov a pomenovanie tých, ktorí na hodine excelovali.

V. Domáca úloha

Naučte sa pravidlá pre vykonávanie aritmetických operácií v dvojkovej číselnej sústave, ako aj tabuľky sčítania, odčítania a násobenia v dvojkovej číselnej sústave.

Nasleduj tieto kroky:

1. 110010 + 111,01;
2. 11110000111 – 110110001;
3. 10101,101 * 111;
4. 10101110/101.

Vytvorte tabuľky sčítania a násobenia v ternárnych a kvinárnych číselných sústavách.

BINÁRNA ARITMETIKA

Pravidlá pre vykonávanie aritmetických operácií s binárnymi číslami sú dané tabuľkami binárneho sčítania, odčítania a násobenia:

Binárne operácie

doplnenie	odčítanie	násobenie
1+1=0+prenos jednotiek

Pravidlá aritmetiky vo všetkých polohových systémoch sú podobné. Pri pridávaní do každej číslice sa v súlade s binárnou sčítacou tabuľkou pridávajú dve číslice výrazov alebo dve z týchto číslic a 1, ak existuje prenos zo susednej číslice nízkeho rádu. Výsledkom je číslica zodpovedajúcej číslice súčtu a prípadne aj 1 prenos na najvýznamnejšiu číslicu. Tu je príklad sčítania dvoch binárnych čísel:

Prestupy

Na pravej strane je sčítanie rovnakých čísel znázornených v desiatkovej sústave.

Pri odčítaní binárnych čísel v danom bite je v prípade potreby obsadený 1 z nasledujúceho najvýznamnejšieho bitu. Táto obsadená 1 sa rovná dvom jednotkám tejto číslice. Pôžička sa poskytuje vždy, keď je číslica v odčítanej číslici väčšia ako číslica na tej istej číslici mínus. Vysvetlime si to na príklade:

Násobenie binárnych viacciferných čísel sa uskutočňuje vytváraním čiastkových súčinov a ich následným sčítaním. V súlade s binárnou tabuľkou násobenia sa každý čiastkový súčin rovná 0, ak zodpovedajúca číslica násobiteľa je 0, alebo sa rovná násobku posunutému o zodpovedajúci počet číslic doľava, ak je číslica násobiteľa 1. , operácia násobenia viacbitových binárnych čísel je zredukovaná na operácie posunu a sčítania. Poloha desatinnej čiarky sa určuje rovnakým spôsobom ako pri násobení desatinných čísel. Ilustruje to príklad:

1011,1 x 101,01 = 111100,011

x 10101

00000 + 10111 00000 10111____

Vlastnosti delenia binárnych čísel sú znázornené na nasledujúcom príklade:

1100,011:10,01 = ? 1100011|10010 -10010 101,1

11011 -10010 10010 -10010 00000

Vďaka jednoduchosti pravidiel binárneho sčítania, odčítania a násobenia umožňuje použitie systému binárnych čísel v počítači zjednodušiť obvody zariadení, ktoré vykonávajú aritmetické operácie.

FORMY REPREZENTÁCIE ČÍSEL V POČÍTAČI

Akékoľvek informácie (čísla, príkazy, alfanumerické záznamy atď.) sú v počítači reprezentované vo forme binárnych kódov (binárnych slov) s pevnou alebo premenlivou dĺžkou. Jednotlivé prvky binárneho kódu, ktoré majú hodnotu 0 alebo 1, sa nazývajú bity. V počítači sú slová často rozdelené na časti nazývané bajty. V moderných počítačoch je široko používaný bajt obsahujúci 8 bitov.

Binárna číslica je v počítači reprezentovaná nejakým technickým zariadením, napríklad spúšťačom, ktorého dva rôzne stavy majú priradené hodnoty 0 a 1. Sada príslušného počtu takýchto zariadení sa používa na reprezentáciu multi- bitové binárne číslo (slovo).

Počítače používajú dve formy reprezentácie čísel: pevná bodka (bodka) a pohyblivá bodka (bodka). Tieto formy sa tiež nazývajú prirodzené a semilogaritmické.

Pri reprezentácii čísel s pevnou bodkou je pozícia desatinnej čiarky pevne stanovená na konkrétnom mieste vzhľadom na číslice čísla. Zvyčajne sa predpokladá, že čiarka je buď pred najvýznamnejšou číslicou alebo za najmenej významnou číslicou. V prvom prípade môžu byť reprezentované iba čísla, ktoré sú v absolútnej hodnote menšie ako 1, v druhom - iba celé čísla.

2-n

					2 -15

< 2 байта, 16 разрядов >

						2 -31

< 4 байта, 32 разрядa >

Dátové formáty na reprezentáciu binárnych čísel s pevnou bodkou (bodkou)

Na obr. Obrázok 1.1 ukazuje príklady dátových formátov na reprezentáciu binárnych čísel s pevnou desatinnou čiarkou a zodpovedajúcich bitových mriežok. Podľa tradície, ktorá sa vyvinula vo výpočtovej technike, sa číslovanie číslic (bitov) v bitovej mriežke vo všeobecných strojoch (počítače ES) vykonáva zľava doprava a v malých počítačoch, mikropočítačoch a mikroprocesoroch - sprava vľavo. Výpustná mriežka zobrazuje hmotnosti výbojov.

Pri reprezentácii čísla so znamienkom je pre kód znamienka pridelený bit "znamienka" (zvyčajne ten úplne vľavo). V tomto bite 0 zodpovedá plusu a 1 mínusu.

Na obr. 1.1 a zobrazuje formát čísel s čiarkou pred najvýznamnejšou číslicou. Tento formát môže predstavovať čísla (správne zlomky) v rozsahu 2–(n-1)

2 –(n-1) |x| 1 – 2 – (n-1)

Prvé počítače boli stroje s pevnou desatinnou čiarkou, pričom čiarka bola fixovaná pred najvýznamnejšou číslicou čísla. V súčasnosti sa na reprezentáciu celých čísel spravidla používa forma s pevnou bodkou (čiarka je pevná za najmenej významnou číslicou).

Existujú dve možnosti reprezentácie celých čísel: so znamienkom a bez znamienka. V druhom prípade všetky číslice bitovej mriežky predstavujú modul čísla.

Znázornenie čísel s pevným bodom sa používa ako hlavné a jediné v strojoch, ktoré sú z hľadiska ich výpočtových možností relatívne malé, používané v systémoch prenosu dát, na riadenie technologických procesov a spracovanie nameraných informácií v reálnom čase.

V strojoch navrhnutých na riešenie širokej škály výpočtových problémov je hlavnou reprezentáciou čísel s pohyblivou rádovou čiarkou, ktorá nevyžaduje škálovanie údajov. Takéto stroje však často okrem tejto formy reprezentácie čísel používajú aj reprezentáciu celých čísel v pevných bodoch, pretože operácie s takýmito číslami sa vykonávajú za kratší čas. Najmä operácie s kódmi adries (indexové aritmetické operácie) sú redukované na operácie s celými číslami.

Reprezentácia čísla s pohyblivou rádovou čiarkou vo všeobecnom prípade má tvar

x = spq; |q|< 1,

kde q je mantisa čísla x, sp je charakteristika čísla X; p - objednávka-, s

Základ charakteristiky (zvyčajne celočíselná mocnina 2).

Mantisa (vlastný zlomok so znamienkom) a exponent (celé číslo so znamienkom) sú reprezentované v číselnej sústave so základom rovným s (v príslušnom binárne kódovanom tvare). Znak čísla sa zhoduje so znakom mantisy.

Poradie p, ktoré môže byť kladné alebo záporné celé číslo, určuje polohu desatinnej čiarky v x.

Na obr. Obrázok 1.2 ukazuje príklady formátov údajov pre čísla s pohyblivou rádovou čiarkou. Jedna časť bitu formátu sa používa na reprezentáciu objednávky a druhá časť sa používa na reprezentáciu mantisy.

Aritmetické operácie s číslami s pohyblivou rádovou čiarkou vyžadujú okrem operácií s mantisami aj určité operácie s príkazmi (porovnávanie, odčítanie atď.). Aby sa zjednodušili operácie s objednávkami, sú zredukované na operácie s kladnými celými číslami (celé čísla bez znamienka), pričom sa používa reprezentácia čísel s pohyblivou rádovou čiarkou s „vysídlený poriadok“.

V prípade reprezentácie čísla s pohyblivou rádovou čiarkou s poradím posunu sa k jeho poradiu p - posun N = 2k pripočíta celé číslo, kde k

Počet binárnych číslic použitých pre modul poriadku. Posunutý rád p cm = p+N je vždy kladný. Na jeho prezentáciu

je potrebný rovnaký počet číslic ako pre modul a znamienko objednávky p. Dôležitou vlastnosťou posunutých zákaziek je, že ak pre

rádov p" a p", ktoré sú celými číslami so znamienkom, je vzťah splnený

potom pre kladné celé čísla zodpovedajúcich posunutých rádov p" cm a p" cm vždy p" cm p" cm. Táto reprezentácia čísla sa tiež nazýva semilogaritmická, pretože časť čísla - charakteristika - je vyjadrená v logaritmickom formulár.

2 ln-2

Objednávkový kód

Kód mantisy

< Длина поля порядка

< Длина поля мантиссы

Znamienko „-“ je kódované ako jedna, znamienko „+“ ako nula.

Reprezentácia s pohyblivou rádovou čiarkou

S pevným počtom číslic mantisy je akákoľvek hodnota v stroji reprezentovaná s najväčšou možnou presnosťou normalizovaným číslom.

Volá sa číslo x = s"q normalizované ak mantisa q spĺňa podmienku

1 > |q| 1/s

t.j. najvýznamnejší bit mantisy v systéme s-ary je odlišný od nuly. Počas procesu výpočtu sa môže získať nenormalizované číslo. V tomto prípade stroj, ak je to predpísané príkazom, ho automaticky normalizuje („normalizovať výsledok“ operácie).

Nech sa r najvýznamnejších bitov s-árnej mantisy rovná 0. Potom normalizácia pozostáva z posunutia mantisy o r bitov doľava a zmenšenia poradia o r jednotiek, pričom 0 sa zapíše do nižších r bitov mantisy. Po tejto operácii sa číslo nezmení a podmienka (2.4) je splnená. S nulovou mantisou je normalizácia nemožná.

Rôzne počítače používajú reprezentáciu čísel s pohyblivou rádovou čiarkou v číselných sústavách s rôznymi základňami, ale rovnajúcimi sa celočíselnej mocnine 2 (s = 2w), pričom poradie p je reprezentované celým číslom a mantisa q je číslo, v ktorom sú skupiny w binárne číslice predstavujú číslice mantisy so základom číselnej sústavy s= 2w.

Príklady použiteľných foriem čísel s pohyblivou rádovou čiarkou s rôznymi základňami číselného systému sú

x = 2p q (1 > |q| 1/2); x=8p q (I > |q| 1/8);

x = 16 p q (I > |q| 1/16).

IN Zodpovedajúce podmienky na získanie normalizovaných čísel sú uvedené v zátvorkách.

Použitie nebinárnej základne pre čísla s pohyblivou rádovou čiarkou trochu znižuje presnosť výpočtov (pre daný počet bitov mantis), ale umožňuje zväčšiť rozsah čísel zastúpených v stroji a urýchliť vykonávanie niektorých operácií, napr. konkrétne

normalizácie, a to z toho dôvodu, že posun možno vykonať o niekoľko binárnych bitov naraz (o štyri bity pre s = 16). Okrem toho sa znižuje pravdepodobnosť výskytu nenormalizovaných čísel počas výpočtov.

Rozsah strojovo reprezentovateľných čísel s pohyblivou rádovou čiarkou závisí od základu číselného systému a počtu číslic pridelených na reprezentáciu poradia. Presnosť výpočtov s pohyblivou rádovou čiarkou je určená počtom číslic v mantise. So zvyšujúcim sa počtom číslic mantisy sa zvyšuje presnosť výpočtov, ale zvyšuje sa aj čas vykonania aritmetických operácií.

Problémy riešené na počítači kladú rôzne nároky na presnosť výpočtov. Preto mnoho strojov používa niekoľko formátov s pohyblivou rádovou čiarkou s rôznym počtom bitov mantisy.

Dopredné, spätné a dodatočné kódy

Aby sa zjednodušili aritmetické operácie, počítače používajú na reprezentáciu čísel špeciálne kódy. Pomocou týchto kódov sa zjednodušuje určenie znamienka výsledku operácie, operácia odčítania (alebo algebraického sčítania) čísel sa zredukuje na aritmetické sčítanie ich kódov a ľahšie sa rozvinú znaky pretečenia čísel. bitová mriežka. V dôsledku toho sú počítačové zariadenia, ktoré vykonávajú aritmetické operácie, zjednodušené.

Na vyjadrenie záporných čísel v počítačoch sa používajú dopredné, inverzné a doplnkové kódy. Kladné čísla sú uvedené v priamom kóde. Vo všetkých týchto kódoch sú číselné číslice a znamienko (úplne vľavo) predstavujúce znamienko čísla, pričom znamienko plus je kódované ako 0 a znamienko mínus ako 1.

Priamy kód binárneho čísla G s (n-1) digitálnymi bitmi je definovaný ako

G pr =		pri G0;
A | G |		pri G 0,

kde A je hodnota rovnajúca sa váhe znamienkového bitu. Pre zlomkové čísla A = 1 a pre celé čísla A = 2n-1.

Pridávanie čísel s rovnakými znakmi v priamom kóde je celkom jednoduché. Čísla sa sčítajú a súčtu sa priradí znakový kód sčítancov. Operácia algebraického sčítania v priamom kóde čísel s rôznymi znamienkami je oveľa zložitejšia. V tomto prípade musíte určiť číslo s veľkým modulom, odpočítať čísla a priradiť rozdielu znamienko väčšieho modulu.

Operácia odčítania (algebraické sčítanie) sa redukuje na operáciu jednoduchého aritmetického sčítania pomocou inverzného a

dodatočné kódy používané na vyjadrenie záporných čísel v stroji.

Ak chcete reprezentovať binárne záporné číslo v spätnom kóde, musíte do bitu znamienka vložiť 1 a vo všetkých ostatných bitoch nahradiť 1 nulami a nuly jednotkami.

Recipročný kód, keď sa naň pozeráme ako na číslo, je modul pôvodného čísla k najväčšiemu číslu bez znamienka, ktoré zapadá do

bitová mriežka. Pre n-bitovú mriežku máme

Go6p=2-2 –(n-1) – lG-l,

ak G- je binárny zlomok a

G- arr = 2n – 1 - |G- |

Keď predstavujete záporné binárne číslo v dvojkovom doplnkovom kóde, umiestnite 1 do znamienka a nahraďte digitálnu časť čísla pridaním modulu čísla k 1 alebo 2n-1 pre zlomky a celé čísla. Je definovaný dvojkový doplnkový kód záporného čísla G

výraz

G- extra =2-|G- |

ak G- je binárny zlomok a

G- extra =2n -|G- |

ak G- je binárne celé číslo.

Recipročné a doplnkové kódy čísla možno považovať za binárne čísla bez znamienok, zatiaľ čo pre binárne zlomky G- add = G- arr + 2-(n- 1) a pre binárne celé čísla C- add = C- arr +1 .

Doplnkový kód čísla teda možno získať z recipročného kódu pridaním 1 k najmenej významnej číslici recipročného kódu.

Pri vykonávaní výpočtov na stroji sa môže vyskytnúť „kladná“ aj „záporná“ 0. Kladná 0 v priamom kóde má tvar

(+0) pr = 000... 0.

Záporná 0 je reprezentovaná v priamom kóde

(- 0)pr = 100...Och,

v opaku

(-0) arr = 111...1;

V dvojkovom doplnkovom kóde nie je záporná 0.

Keď sú kladné čísla reprezentované priamym kódom a záporné čísla ďalšou nulou, existuje jeden obrázok. Pri použití spätného kódu majú „kladná“ a „záporná“ 0 rôzne obrázky.

Zmena znamienka záporného čísla zodpovedá invertovaniu jeho kódu, ak je číslo uvedené v opačnom kóde, a invertovaniu a

pridanie 1 najmenšej platnej číslice, ak je záporné číslo zastúpené v dvojke. Výsledkom je priamy kód pre zodpovedajúce kladné číslo. Vyššie uvedené vyplýva zo vzťahov:

pre zlomky

G- pr = |G- | = 2 – 2-(n-1) – G- arr -G- av = |G- | = 2 – G-add

pre celé čísla

G- pr = |G- | = 2n – 1 – G- arr -G- arr = |G- | = 2n – G- prid

Uvažujme o použití inverzných a doplnkových kódov pri algebraickom sčítaní n-bitových binárnych čísel G a Q, keď jedno z nich alebo obe čísla sú záporné. Je možné sformulovať nasledujúce pravidlá (predpokladáme, že modul algebraického súčtu je menší ako 1 pre zlomky a menší ako 2n-1 pre celé čísla, a preto je možné súčtový kód znázorniť v n-cifernej sieti).

Pri algebraickom sčítaní dvoch binárnych čísel pomocou spätného (alebo doplnkového) kódu sú kladné členy zastúpené v priamom kóde a záporné v opačnom (doplnkovom) kóde a vykonáva sa aritmetický súčet týchto kódov vrátane znamienkových bitov. ktoré sa považujú za najvyššie číslice. Keď dôjde k prenosu zo znamienkového bitu, prenosová jednotka sa pri použití spätného kódu pridá k bitu nižšieho rádu súčtu kódov a pri použití doplnkového kódu sa zahodí. Výsledkom je algebraický súčet v priamom kóde, ak je tento súčet kladný, a v opačnom (doplnkovom) kóde, ak je záporný.

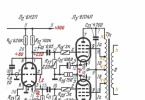
Predpokladajme, že musíte vykonať dve operácie: 176154 a 176215

V prvom prípade bude výsledok pozitívny av druhom - negatívny. Preveďme tieto čísla do binárneho kódu napríklad cez

osmičkový systém.
17610 =2608				15410 =2328			21510 =3278

0101100002 0100110102 0110101112

invertovať subtrahendy na recipročné a komplementárne kódy